what is the area of triangle abc? round to the nearest square unit. square units
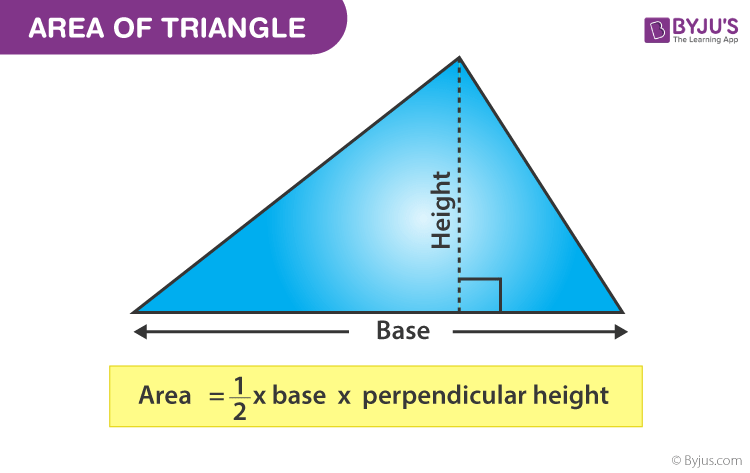
Expanse of a triangle is the region enclosed by it, in a two-dimensional airplane. Equally we know, a triangle is a airtight shape that has three sides and three vertices. Thus, the surface area of a triangle is the total infinite occupied within the 3 sides of a triangle. The general formula to detect the surface area of the triangle is given by half of the product of its base and tiptop.
In full general, the term "expanse" is divers as the region occupied within the boundary of a flat object or figure. The measurement is done in foursquare units with the standard unit of measurement being square meters (k2). For the computation of expanse, at that place are pre-defined formulas for squares, rectangles, circle, triangles, etc. In this article, nosotros volition acquire the expanse of triangle formulas for different types of triangles, along with some example problems.
What is Surface area of a Triangle?
The area of a triangle is defined as the total region that is enclosed past the three sides of whatever particular triangle. Basically, it is equal to one-half of the base of operations times height, i.e. A = ane/2 × b × h. Hence, to find the surface area of a tri-sided polygon, we have to know the base (b) and superlative (h) of it . It is applicable to all types of triangles , whether it is scalene, isosceles or equilateral. To be noted, the base and superlative of the triangle are perpendicular to each other. The unit of expanse is measured in square units (chiliad 2 , cm 2 ).
Case: What is the area of a triangle with base b = three cm and height h = iv cm?
Using the formula,
Area of a Triangle, A = ane/ii× b × h = ane/2×4 cm×three cm = 2 cm×three cm = 6 cm2
Apart from the above formula, we accept Heron's formula to calculate the triangle'due south area, when nosotros know the length of its three sides. Also, trigonometric functions are used to find the area when nosotros know ii sides and the angle formed between them in a triangle. Nosotros will calculate the area for all the weather given here.
Area of a Triangle Formula
The area of the triangle is given by the formula mentioned below:
Area of a Triangle = A = ½ (b × h) square units
where b and h are the base and superlative of the triangle, respectively.
Now, let's see how to calculate the area of a triangle using the given formula. The area formulas for all the different types of triangles like an area of an equilateral triangle, right-angled triangle, an isosceles triangle are given below. Also, how to find the area of a triangle with 3 sides using Heron'due south formula with examples.
Surface area of a Correct Angled Triangle
A right-angled triangle, besides called a right triangle has one bending at 90° and the other two astute angles sums to 90°. Therefore, the height of the triangle will be the length of the perpendicular side.

Area of a Correct Triangle = A = ½ × Base of operations × Peak (Perpendicular distance)
From the above figure,
Area of triangle ACB = 1/2 ab
Area of an Equilateral Triangle
An equilateral triangle is a triangle where all the sides are equal. The perpendicular fatigued from the vertex of the triangle to the base divides the base into two equal parts. To summate the area of the equilateral triangle, we have to know the measurement of its sides.

- Area of an Equilateral Triangle = A = (√3)/4 × sidetwo
Area of an Isosceles Triangle
An isosceles triangle has two of its sides equal and also the angles opposite the equal sides are equal.

- Surface area of an Isosceles Triangle = i/iv b√(4a2 – b2)
Perimeter of a Triangle
The perimeter of a triangle is the altitude covered around the triangle and is calculated by adding all three sides of a triangle.
- The perimeter of a triangle = P = (a + b + c) units
where a, b and c are the sides of the triangle.
Expanse of Triangle with Three Sides (Heron'south Formula)
The area of a triangle with 3 sides of different measures can be found using Heron'southward formula . Heron's formula includes ii important steps. The first step is to find the semi perimeter of a triangle by adding all the iii sides of a triangle and dividing it by 2. The adjacent step is that, apply the semi-perimeter of triangle value in the main formula called "Heron's Formula" to find the area of a triangle.
 where, s is semi-perimeter of the triangle = s = (a+b+c) / 2
where, s is semi-perimeter of the triangle = s = (a+b+c) / 2
We take seen that the area of special triangles could be obtained using the triangle formula. However, for a triangle with the sides existence given, the calculation of height would not be uncomplicated. For the aforementioned reason, we rely on Heron's Formula to calculate the area of the triangles with diff lengths.
Area of a Triangle Given Two Sides and the Included Bending (SAS)
At present, the question comes, when we know the two sides of a triangle and an bending included between them, then how to observe its surface area.
Permit u.s.a. take a triangle ABC, whose vertex angles are ∠A, ∠B, and ∠C, and sides are a,b and c, as shown in the figure below.
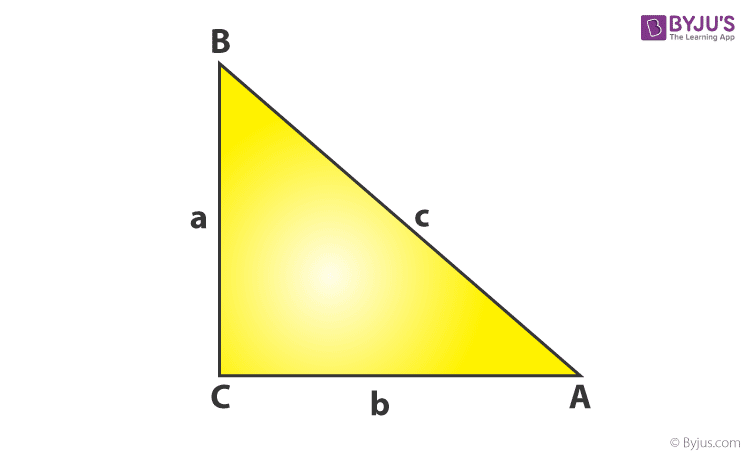
Now, if whatever two sides and the angle betwixt them are given, and then the formulas to calculate the area of a triangle is given past:
Area (∆ABC) = ½ bc sin A
Expanse (∆ABC) = ½ ab sin C
Expanse (∆ABC) = ½ ca sin B
These formulas are very easy to retrieve and also to calculate.
For example, If, in ∆ABC, A = xxx° and b = ii, c = 4 in units. And then the surface area will be;
Area (∆ABC) = ½ bc sin A
= ½ (ii) (iv) sin thirty
= four x ½ (since sin 30 = ½)
= two sq.unit of measurement.
Related Manufactures
- Expanse Of Isosceles Triangle
- Expanse Of Scalene Triangle
- Expanse Of Similar Triangles
- Properties Of Triangle
- Perimeter of Triangle
- Heron'southward Formula
Area of a Triangle Solved Examples
Example ane:
Notice the area of an acute triangle with a base of 13 inches and a height of five inches.
Solution:
A = (½)× b × h sq.units
⇒ A = (½) × (13 in) × (v in)
⇒ A = (½) × (65 inii)
⇒ A = 32.v in2
Example 2:
Detect the expanse of a correct-angled triangle with a base of vii cm and a height of eight cm.
Solution:
A = (½) × b × h sq.units
⇒ A = (½) × (7 cm) × (8 cm)
⇒ A = (½) × (56 cm2)
⇒ A = 28 cm2
Case 3:
Find the surface area of an obtuse-angled triangle with a base of 4 cm and a height vii cm.
Solution:
A = (½) × b × h sq.units
⇒ A = (½) × (iv cm) × (7 cm)
⇒ A = (½) × (28 cm2)
⇒ A = 14 cm2
Oft Asked Questions on Area of a Triangle
What is the area of a triangle?
The expanse of the triangle is the region enclosed past its perimeter or the 3 sides of the triangle.
What is the area when ii sides of a triangle and included angle are given?
The area volition be equal to half times of the product of two given sides and sine of the included bending.
How to find the area of a triangle given three sides?
When the values of the three sides of the triangle are given, then we can notice the surface area of that triangle by using Heron'south Formula. Refer to the section 'Expanse of a triangle past Heron's formula' mentioned in this article to get a complete idea.
How to find the area of a triangle using vectors?
Suppose vectorsu and v are forming a triangle in space. Then, the area of this triangle is equal to half of the magnitude of the product of these two vectors, such that,
A = ½ |u × 5|
How to calculate the area of a triangle?
For a given triangle, where the base of the triangle is b and height is h, the area of the triangle can be calculated by the formula, such as;
A = ½ (b × h) Square Unit
schindlerconereven.blogspot.com
Source: https://byjus.com/maths/area-of-a-triangle/
0 Response to "what is the area of triangle abc? round to the nearest square unit. square units"
Post a Comment